Скачайте изображение (превью) выбрав качество

320x180 480x360 640x480 1280x720

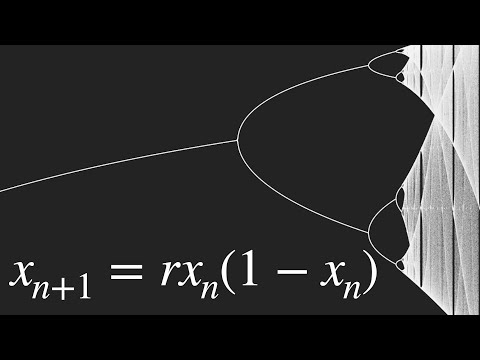
The logistic map connects fluid convection, neuron firing, the Mandelbrot set and so much more. Fasthosts Techie Test competition is now closed! Learn more about Fasthosts here: Code for interactives is available below...

Animations, coding, interactives in this video by Jonny Hyman 🙌
Try the code yourself:

References:
James Gleick, Chaos
Steven Strogatz, Nonlinear Dynamics and Chaos

May, R. Simple mathematical models with very complicated dynamics. Nature 261, 459–467 (1976).

Robert Shaw, The Dripping Faucet as a Model Chaotic System


Crevier DW, Meister M. Synchronous period-doubling in flicker vision of salamander and man.
J Neurophysiol. 1998 Apr;79(4):1869-78.

Bing Jia, Huaguang Gu, Li Li, Xiaoyan Zhao. Dynamics of period-doubling bifurcation to chaos in the spontaneous neural firing patterns Cogn Neurodyn (2012) 6:89–106 DOI 10.1007/s11571-011-9184-7

A Garfinkel, ML Spano, WL Ditto, JN Weiss. Controlling cardiac chaos
Science 28 Aug 1992: Vol. 257, Issue 5074, pp. 1230-1235 DOI: 10.1126/science.1519060

R. M. May, D. M. G. Wishart, J. Bray and R. L. Smith Chaos and the Dynamics of Biological Populations
Source: Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 413, No. 1844, Dynamical Chaos (Sep. 8, 1987), pp. 27-44

Chialvo, D., Gilmour Jr, R. & Jalife, J. Low dimensional chaos in cardiac tissue. Nature 343, 653–657 (1990).

Xujun Ye, Kenshi Sakai. A new modified resource budget model for nonlinear dynamics in citrus production. Chaos, Solitons and Fractals 87 (2016) 51–60

Libchaber, A. & Laroche, C. & Fauve, Stephan. (1982). Period doubling cascade in mercury, a quantitative measurement. . 43. 10.1051/jphyslet:01982004307021100.

Special thanks to Patreon Supporters:
Alfred Wallace, Arjun Chakroborty, Bryan Baker, DALE HORNE, Donal Botkin, halyoav, James Knight, Jasper Xin, Joar Wandborg, Lee Redden, Lyvann Ferrusca, Michael Krugman, Pindex, Ron Neal, Sam Lutfi, Tige Thorman, Vincent

Special thanks to:
Henry Reich for feedback on earlier versions of this video
Raquel Nuno for enduring many earlier iterations (including parts she filmed that were replaced)
Dianna Cowern for title suggestions and saying earlier versions weren't good
Heather Zinn Brooks for feedback on an earlier version.


Music from:
"What We Discovered" "A Sound Foundation 1" "Seaweed" "Colored Spirals 4"

"Busy World" "Children of Mystery"

Чтобы скачать видео "This equation will change how you see the world (the logistic map)" передвинте ползунок вправо